螺栓連接結(jié)構(gòu)廣泛應(yīng)用于航空航天、鐵路運(yùn)輸?shù)却笮蛷?fù)雜裝備中,其連接結(jié)構(gòu)處于復(fù)雜裝備內(nèi)部,工作時(shí)無法實(shí)時(shí)監(jiān)測(cè)性能狀態(tài)[1-3]�。同時(shí)設(shè)備間存在大量結(jié)構(gòu)跨尺度和非線性問題�,導(dǎo)致分析螺栓連接結(jié)構(gòu)動(dòng)力學(xué)響應(yīng)較為困難,對(duì)裝備的可靠性���、安全性造成了困擾。研究學(xué)者將有限元方法(FEA)廣泛應(yīng)用到復(fù)雜裝備的性能計(jì)算����、壓強(qiáng)表征中可通過有限元軟件建立螺栓連接結(jié)構(gòu)接觸模型分析其性能,彌補(bǔ)無法直接測(cè)量的困難���。
裝備在存儲(chǔ)���、運(yùn)輸、使用過程���,由于振動(dòng)���、碰撞等因素,導(dǎo)致裝備受到切向外力的影響����,進(jìn)而影響裝備接觸狀態(tài)����。接觸狀態(tài)的變化研究對(duì)保障結(jié)構(gòu)安全�����、預(yù)測(cè)和評(píng)估結(jié)構(gòu)壽命����、優(yōu)化結(jié)構(gòu)設(shè)計(jì)具有重要意義。局部接觸區(qū)域和壓強(qiáng)過高�����,可能導(dǎo)致復(fù)雜裝備發(fā)生疲勞����、塑性形變,影響整個(gè)結(jié)構(gòu)的安全[4]��。因此�����,對(duì)切向外載荷作用下的螺栓連接接觸狀態(tài)分析具有重要作用。
研究學(xué)者將接觸邊界分為圓形[5]�����、橢圓形[6]��。無切向外力時(shí)�,接觸邊界為圓形。隨切向力的作用��,接觸邊界逐步演化為橢圓形����。接觸壓強(qiáng)分布可表征為赫茲壓強(qiáng)分布�����、Fernlund壓強(qiáng)分布����、線性壓強(qiáng)分布等。Li[7,8]利用粗糙表面的赫茲壓強(qiáng)分布表征接觸表面的壓強(qiáng)變化���,構(gòu)建了密度函數(shù)���,并通過實(shí)驗(yàn)驗(yàn)證了方法的正確性���。此方法能較好表征接觸面壓強(qiáng)分布規(guī)律,但其未知參數(shù)較多�����,導(dǎo)致計(jì)算較為復(fù)雜���。Wang[6]基于Fernlund壓強(qiáng)4次分布函數(shù)����,研究了隨切向力變化的動(dòng)態(tài)壓強(qiáng)分布函數(shù)����,分析了接觸狀態(tài)變化。但計(jì)算公式較為復(fù)雜�,待辨識(shí)參數(shù)較多。
Zhao[5]假設(shè)研究了參數(shù)較少的線性壓強(qiáng)分布�,構(gòu)建了不考慮接觸狀態(tài)演化的線性壓強(qiáng)分布函數(shù)。因此����,急需建立可準(zhǔn)確表征連接界面接觸邊界�����、面積的數(shù)學(xué)函數(shù)�,表征接觸邊界變化規(guī)律���。構(gòu)建考慮切向載荷影響的動(dòng)態(tài)壓強(qiáng)分布函數(shù)�����,將接觸狀態(tài)演化引入到分布函數(shù)中�。
綜上���,切向載荷作用下連接界面產(chǎn)生接觸邊界����、壓強(qiáng)分布變化���,對(duì)動(dòng)力學(xué)特性造成一定影響。為簡(jiǎn)化壓強(qiáng)分布函數(shù)�,提高函數(shù)預(yù)測(cè)的準(zhǔn)確性,本文建立了高精度有限元模型�����,研究了接觸邊界變化規(guī)律,分析結(jié)合面的多種壓強(qiáng)分布函數(shù)�����。構(gòu)建了參數(shù)較少����、表征效果較好的切向力動(dòng)態(tài)變化線性壓強(qiáng)分布函數(shù)。有助于為螺栓連接的力學(xué)行為和接觸機(jī)理提供理論支撐�。
1、簡(jiǎn)化螺栓和平板建模方法研究
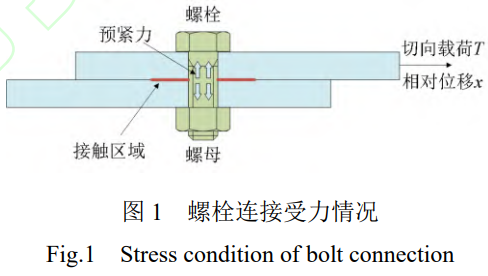
混合載荷耦合作用下�,螺栓連接與平板接觸面受力情況如圖1所示。核級(jí)設(shè)備具有特殊性����、復(fù)雜性,其內(nèi)部存在大量螺栓連接結(jié)構(gòu)����。以復(fù)雜裝備中高強(qiáng)度合金鎳鋼材料為基礎(chǔ),鎳鋼平板具有高強(qiáng)度�����、高硬度、耐腐蝕性的特點(diǎn)�����,廣泛應(yīng)用于航空發(fā)動(dòng)機(jī)等多種重要的復(fù)雜裝備中�����。然而�����,由于填充系數(shù)較低����,現(xiàn)有普通裝備中較少使用此材料,目前領(lǐng)域內(nèi)對(duì)于鎳鋼材料的研究較少�。因此,本文聚焦于復(fù)雜裝備中鎳鋼結(jié)構(gòu)���,以L形平板為對(duì)象,簡(jiǎn)化了裝備的復(fù)雜程度����,避免其它部件對(duì)動(dòng)力學(xué)特性產(chǎn)生影響��。選取GB/T5783-2016[9]標(biāo)準(zhǔn)的8.8級(jí)M8×36標(biāo)準(zhǔn)外六角螺栓作為研究對(duì)象��。
1.1螺栓緊固件建模
基于Solidworks軟件建立帶升角螺栓���,將螺紋與螺母的相互作用通過ABAQUS軟件嚙合,可模擬螺栓工作時(shí)的受力方向�����,提高分析的準(zhǔn)確性���?��;诼菟ㄖ行悦嫣砑宇A(yù)緊力,可簡(jiǎn)化計(jì)算的復(fù)雜程度���。螺距P為1mm����,螺栓頭部?jī)?nèi)切圓半徑為6.5mm���,厚度k為5.15mm�����,對(duì)角長度e為14.38mm��。為簡(jiǎn)化螺紋建模復(fù)雜程度�,提高ABAQUS分析效率和收斂性,采用光滑螺桿替代螺紋并將螺栓頭部簡(jiǎn)化為圓面���。網(wǎng)格質(zhì)量極大影響計(jì)算結(jié)果��,ABAQUS軟件可自動(dòng)劃分四面體�����、六面體網(wǎng)格���。螺紋處網(wǎng)格與平面處不同,存在多處的凹凸面����。因此,本文采用Hypermesh軟件對(duì)螺紋處進(jìn)行手動(dòng)繪制高精密網(wǎng)格�,確保每一處網(wǎng)格呈現(xiàn)均勻六面體形狀�����,如圖2所示。精密網(wǎng)格可避免模型不收斂的問題�,有效控制計(jì)算誤差。

1.2等效連接平板建模
為避免轉(zhuǎn)矩對(duì)螺栓產(chǎn)生的影響���,將平板簡(jiǎn)化為L形����,如圖3所示���。平板的孔需略大于螺栓直徑���。因此將平板的螺孔直徑調(diào)整為9mm,保證平板未受力前����,二者不接觸。通過ABAQUS自帶網(wǎng)格編輯器���,調(diào)整鎳鋼平板的網(wǎng)格為四面體網(wǎng)格�����,對(duì)螺栓頭部����、螺孔接觸面進(jìn)行網(wǎng)格細(xì)分,提高計(jì)算精度�����。將材料假定為純彈性���,當(dāng)外力工作結(jié)束后����,材料不存在殘余形變����,可恢復(fù)為原狀態(tài)。設(shè)置材料的泊松比為0.291�,屈服應(yīng)力590MPa,彈性模量為205.9GPa�����,楊氏模量143GPa。

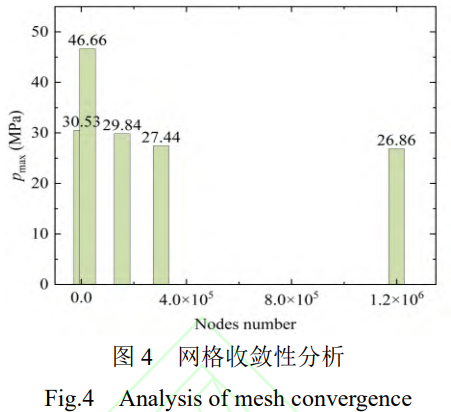
為提高計(jì)算的準(zhǔn)確性��,對(duì)模型進(jìn)行了網(wǎng)格檢驗(yàn)�����,模型節(jié)點(diǎn)數(shù)量與最大接觸壓強(qiáng)的關(guān)系如圖4所示���。分別劃分了0.5mm、0.8mm����、1mm、2mm�����、5mm單元尺寸的網(wǎng)格����。當(dāng)網(wǎng)格大小為0.5mm-0.8mm時(shí),最大壓強(qiáng)趨于穩(wěn)定在26-27MPa�����,表明模型網(wǎng)格已趨于穩(wěn)定,精確度較高���。然而0.5mm單元節(jié)點(diǎn)數(shù)量較0.8mm單元節(jié)點(diǎn)數(shù)量增加了89萬����,降低了計(jì)算效率�。因此采用0.8mm單元尺寸的網(wǎng)格。
1.3有限元載荷���、邊界條件及分析步設(shè)置
ABAQUS軟件中施加螺栓預(yù)緊載荷的方式有多種:①在螺栓中性面添加固定當(dāng)前長度的預(yù)緊載荷��。②基于熱膨脹原理采用降溫法�����,通過施加螺栓負(fù)溫度的形式�,使得螺桿收縮產(chǎn)生預(yù)緊力�。③基于螺紋與螺母的嚙合,通過旋轉(zhuǎn)螺母的形式施加預(yù)緊�。④直接壓縮螺桿的長度,使螺桿具有法向的壓縮力�,即可表征為預(yù)緊載荷。上述方法中除第一種外���,均難以控制首次施加的預(yù)緊載荷的大小����,因此我們選取第一種施加預(yù)緊載荷的方式,以達(dá)到高精度預(yù)緊設(shè)置�����。
通過位移載荷替代切向力����,可提高計(jì)算結(jié)果的精確性�。對(duì)右側(cè)平板面施加耦合作用,得到耦合點(diǎn)�。提取耦合點(diǎn)的位移和反作用力可得出相對(duì)應(yīng)的載荷。左側(cè)平板面施加固定約束��,模擬復(fù)雜裝備的工作狀態(tài)���,使得分析步能夠合理運(yùn)行����。
螺栓與平板存在多處接觸面:螺栓頭部下表面���、螺母上表面與平板的接觸�、螺紋與螺母的接觸、平板間的接觸�����。在設(shè)定接觸面時(shí)��,需考慮網(wǎng)格質(zhì)量�、接觸面的形狀、材料的影響����。設(shè)置三個(gè)基礎(chǔ)分析步:第一步施加10-100N較小預(yù)緊載荷,提高計(jì)算結(jié)果的收斂性����。第二步施加所需預(yù)緊載荷。第三步在右側(cè)平板的耦合點(diǎn)施加所需x方向的位移����,以模擬切向力的作用。若要進(jìn)行多組拉伸���、壓縮循環(huán)加載分析��,可增加多組分析步���。
2��、接觸邊界變化規(guī)律研究
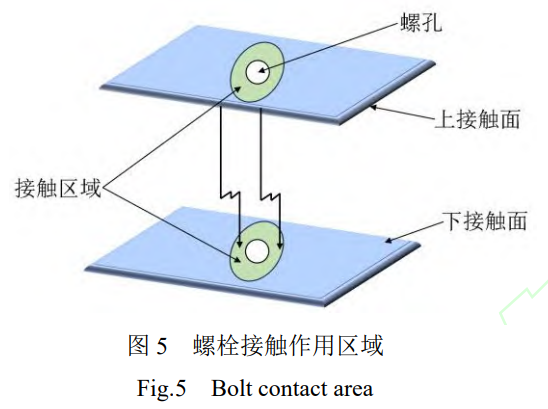
平板間上下結(jié)合面接觸時(shí)���,存在局部的接觸區(qū)域,并非整個(gè)面完全接觸�����,如圖5所示�。主要接觸區(qū)域?yàn)槁菘字車?��,其壓力分布并不完全均勻�����,受到變形程度�����、材質(zhì)的影響���。在切向載荷的作用下���,接觸區(qū)域形狀逐漸變化。為研究接觸區(qū)域的邊界演化規(guī)律���,通過有限元方法分析接觸邊界��,構(gòu)建可表征粘滯��、滑移區(qū)域的邊界函數(shù)�。
連接表面的滑動(dòng)狀態(tài)分為四種:粘滯�����、微滑�、宏滑、銷連�,無外力作用下,難以引起螺孔周圍接觸區(qū)域移動(dòng)�,稱為粘滯狀態(tài)。微滑����、宏滑狀態(tài)分別指較小����、較大載荷下導(dǎo)致接觸面相對(duì)滑動(dòng)����。銷連狀態(tài)發(fā)生彈性形變,影響結(jié)構(gòu)的安全性�����。施加1000N預(yù)緊力��,0-829N的切向位移載荷�。當(dāng)切向載荷T≤261N時(shí),無切向力情況螺孔周圍呈現(xiàn)圓形粘滯狀態(tài)���,伴隨切向力的施加,粘滯區(qū)域逐漸減小�����,接觸形態(tài)由圓形逐漸演化為橢圓狀��。當(dāng)切向載荷T≥261N時(shí),接觸區(qū)域由粘滯狀態(tài)逐漸過渡至滑移狀態(tài)���,滑移區(qū)域不斷從外部向內(nèi)部延伸����,x方向滑移長度縮短��,y方向滑移長度增加�����,接觸區(qū)域超過平板邊界��,平板對(duì)接觸區(qū)域產(chǎn)生“截?cái)唷爆F(xiàn)象�����。
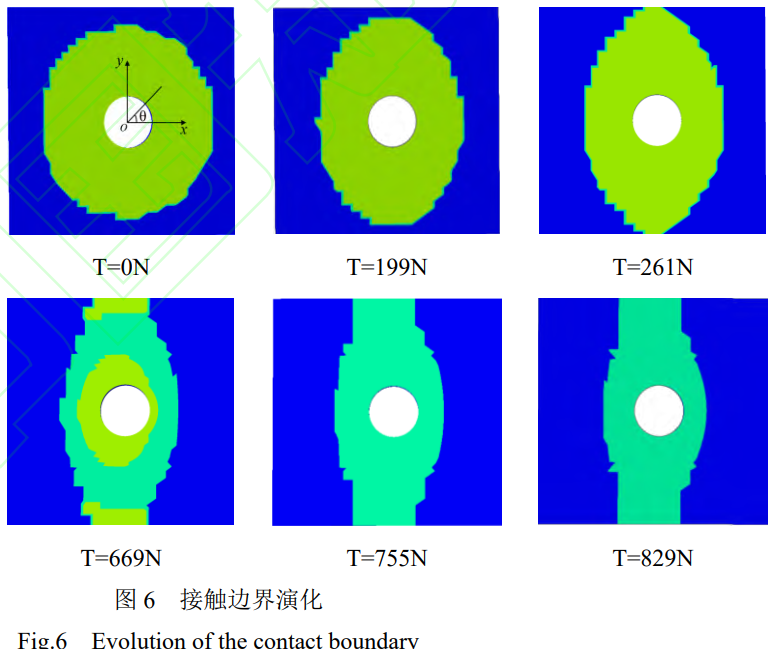
無切向載荷條件下�,接觸區(qū)域呈圓形。切向力作用下�,平板間的接觸區(qū)域可近似為橢圓形。將切向拉力方向定義為x�����,垂直方向?yàn)閥,因此���,將接觸邊界形狀近似為橢圓狀��,其公式為
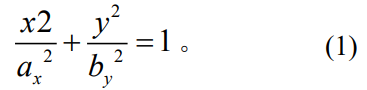
伴隨切向位移載荷的增大�,接觸邊界逐漸變化���,短半軸縮短���,長半軸增加,并超過平板最大寬度��。依據(jù)有限元模型辨ax�����、by圖7所示����。
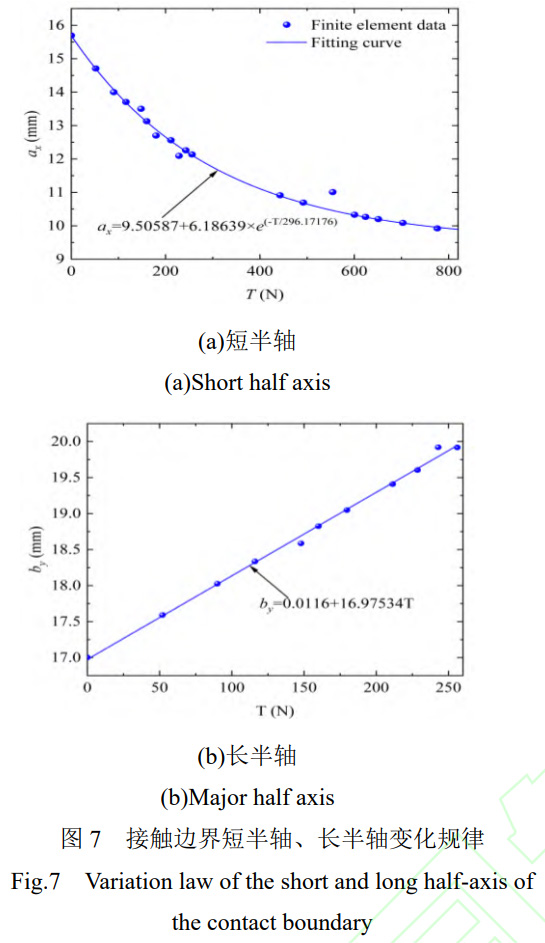
短半軸數(shù)值隨著切向載荷的增大而減小,長半軸數(shù)值隨著切向載荷的增大而增大���。短半軸函數(shù)符合指數(shù)變化,長半軸函數(shù)符合線性變化,其通用公式為
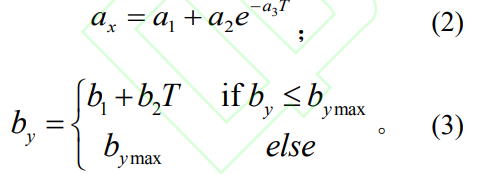
式中:a1��、a2�����、a3�、b1、b2均為待辨識(shí)參數(shù)��;bymax為長半軸的最大值��,可通過有限元進(jìn)行參數(shù)辨識(shí)����。
基于式(2)和(3),可通過橢圓面積求得接觸面積為
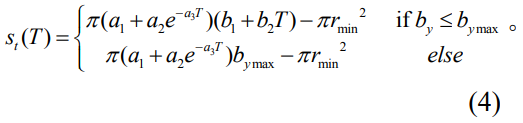
通過長半軸變化公式可知���,當(dāng)T≤261時(shí)����,接觸區(qū)域逐漸演化����,未達(dá)到最大長半軸�。當(dāng)T≥261時(shí)���,平板結(jié)合面出現(xiàn)截?cái)鄥^(qū)域���,通過上述公式計(jì)算的橢圓接觸面積偏小。
3��、壓強(qiáng)變化規(guī)律研究
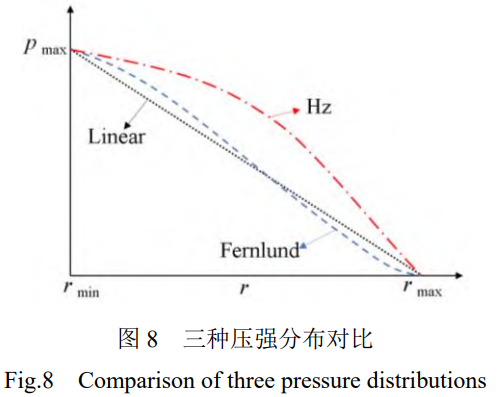
螺栓連接在預(yù)緊力作用下����,使得平板產(chǎn)生壓強(qiáng),施加切向外載荷導(dǎo)致壓強(qiáng)發(fā)生變化����。基于現(xiàn)有模型函數(shù)描述壓強(qiáng)分布規(guī)律�����,可表征真實(shí)壓強(qiáng)分布規(guī)律���,常用壓強(qiáng)分布函數(shù)包括:Fernlund壓強(qiáng)分布[10]����、線性壓強(qiáng)分布[5]、赫茲壓強(qiáng)分布[11]����。通過高精密有限元模型����,計(jì)算平板間壓強(qiáng)分布數(shù)值,并通過分布函數(shù)簡(jiǎn)化壓強(qiáng)分布規(guī)律�。
3.1壓強(qiáng)分布函數(shù)
(1)Fernlund壓強(qiáng)分布Motosh將壓強(qiáng)與半徑表示為4次方程,構(gòu)建了螺栓連接節(jié)點(diǎn)剛度確定方法���,其表達(dá)式為
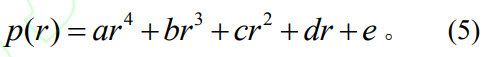
式中:
p(r)為壓強(qiáng)�;r為壓強(qiáng)點(diǎn)到螺孔邊緣的距離���。
基于公式(5)����,可構(gòu)建接觸表面法向總預(yù)緊力的表達(dá)式
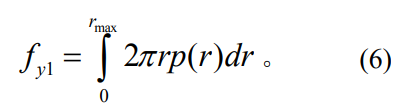
2)線性壓強(qiáng)分布
基于壓強(qiáng)與半徑的因果關(guān)系���,將分布規(guī)律理想化��,建立一元線性回歸���,可采用最小二乘法辨識(shí)線性分布中的參數(shù)��,其表達(dá)式為
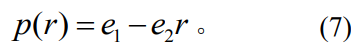
(3)赫茲壓強(qiáng)分布
赫茲壓強(qiáng)分布基于兩個(gè)接觸物體之間變形假設(shè)理論����,將模型簡(jiǎn)化為剛體和面積較小的微凸體接觸�。壓強(qiáng)峰值位移接觸中心點(diǎn),并逐漸向遠(yuǎn)距離處減小�����。其壓強(qiáng)分布的建立需通過多種物體間假設(shè)��、簡(jiǎn)化�,與實(shí)際情況之間存在誤差,其表達(dá)式為
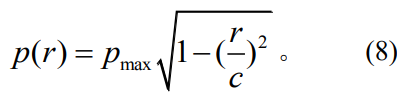
3.2基于有限元的壓強(qiáng)函數(shù)辨識(shí)
有限元模型中施加1000N-15000N法向預(yù)緊力�,設(shè)置切向位移載荷0.05mm,求解上����、下平板接觸面間壓強(qiáng)分布規(guī)律。以x方向的螺孔邊緣處為原點(diǎn)�,即為r=0處,分別提取切向拉力方向壓強(qiáng)數(shù)值,如圖9所示��。較小預(yù)緊力情況下�,三種壓強(qiáng)分布函數(shù)均表征較好。較大預(yù)緊力情況下����,三種壓強(qiáng)分布函數(shù)均在螺孔邊緣處存在偏差���,螺孔周圍為應(yīng)力集中區(qū)域����,當(dāng)預(yù)緊載荷較大時(shí)��,可能會(huì)使得材料的力學(xué)性能發(fā)生改變���,例如彈性模量��、屈服強(qiáng)度等���。由于螺孔的存在,改變了平板的剛度分布��,使得螺孔邊緣的剛度變化較大�。結(jié)合面的摩擦系數(shù)等因素在較大預(yù)緊工況下也會(huì)對(duì)壓強(qiáng)分布產(chǎn)生一定影響�����,導(dǎo)致壓強(qiáng)分布函數(shù)在此位置偏差較大���。線性壓強(qiáng)與Fernlund壓強(qiáng)分布在螺孔最遠(yuǎn)處均存在偏差。而赫茲壓強(qiáng)分布偏差較大�����,不符合有限元中平板接觸壓強(qiáng)分布規(guī)律�。
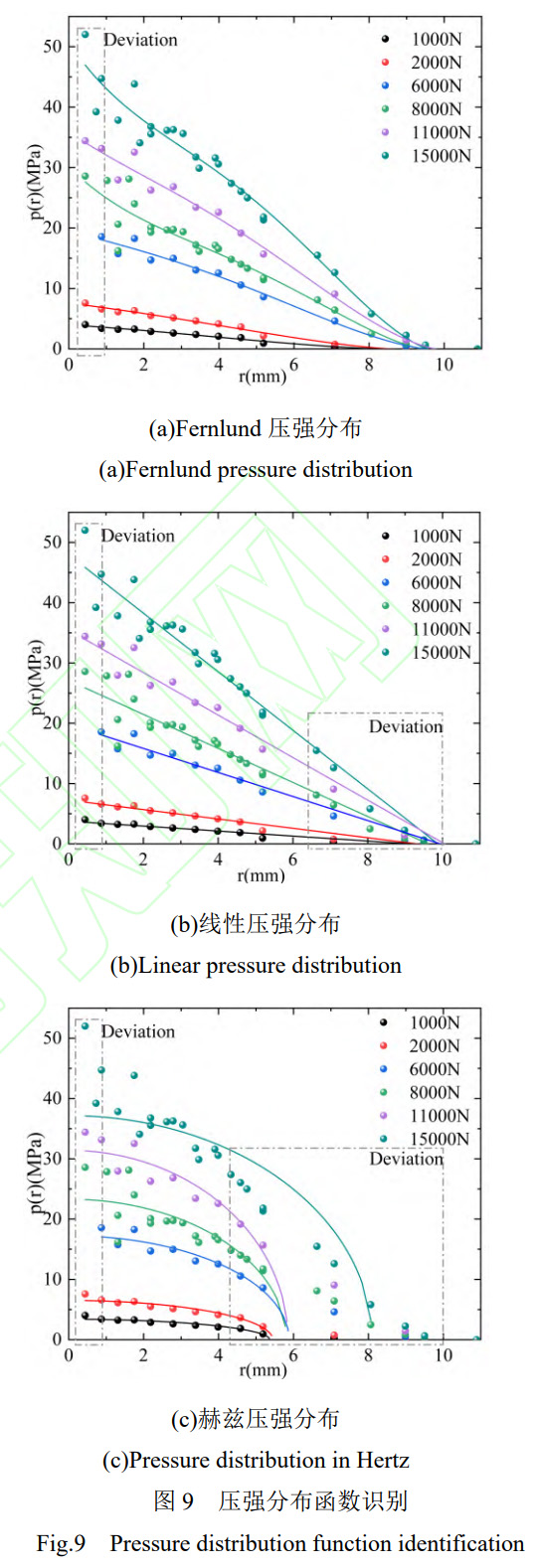
不同初始預(yù)緊力下,由偏離區(qū)域可知�����,二者擬合精度相近�,均可表征螺栓連接接觸表面壓強(qiáng)分布。
Fernlund壓強(qiáng)分布函數(shù)為四次函數(shù)���,包含5個(gè)未知參數(shù)����,而線性壓強(qiáng)分布僅存在2個(gè)未知參數(shù),可簡(jiǎn)化計(jì)算����。因此,選取參數(shù)較少���,表征效果較好�,結(jié)構(gòu)簡(jiǎn)單的線性函數(shù)作為壓強(qiáng)分布函數(shù)�����。
3.3動(dòng)態(tài)壓強(qiáng)分布函數(shù)研究
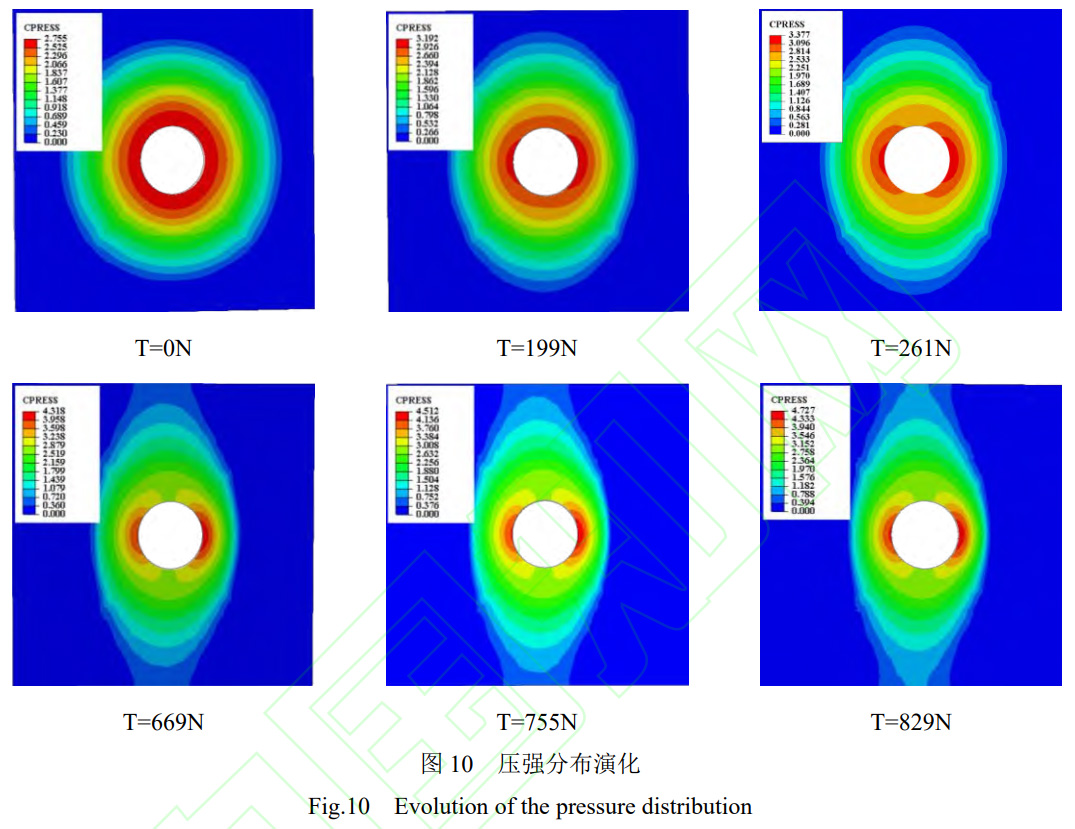
1000N法向預(yù)緊載荷���、切向0-829N切向外載荷作用下的壓強(qiáng)變化如圖10所示。較小外載荷作用下����,接觸區(qū)域呈對(duì)稱分布,較大外載荷作用下����,其壓強(qiáng)峰值對(duì)稱分布在y軸兩側(cè)。隨切向力的增加�,壓強(qiáng)最大值由2.755MPa變化至4.727MPa,增長率達(dá)到71.6%。因此構(gòu)建平板間動(dòng)態(tài)壓強(qiáng)分布規(guī)律�,需考慮切向外載荷的影響。
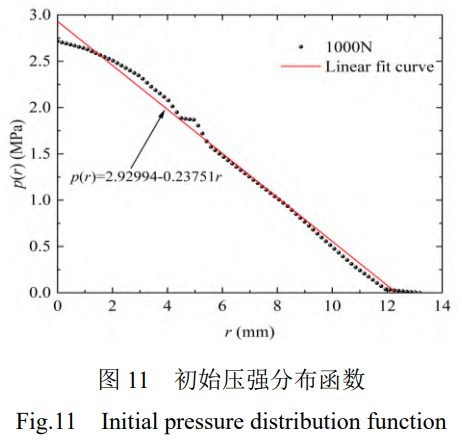
T=0時(shí)���,1000N法向預(yù)緊載荷作用下���,基于有限元對(duì)線性壓強(qiáng)參數(shù)1e、2e進(jìn)行辨識(shí)�,如圖11所示。線性壓強(qiáng)分布在r=0mm時(shí)的誤差為7.9%�,在r=4mm時(shí)的誤差為5.0%,具有較好的擬合效果����。
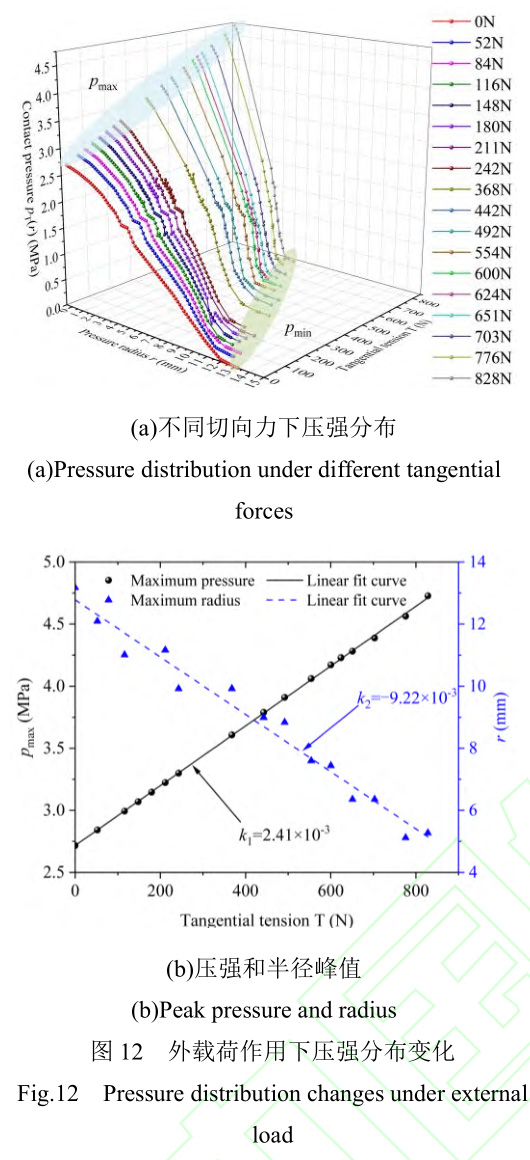
線性壓強(qiáng)分布函數(shù)可描述平板間壓強(qiáng)演化規(guī)律,而切向力的改變會(huì)導(dǎo)致最大壓強(qiáng)值���、壓強(qiáng)最大半徑變化�����,對(duì)x軸正方向的壓強(qiáng)展開有限元分析�����,如圖12(a)所示��。當(dāng)壓強(qiáng)半徑r=0時(shí)�����,壓強(qiáng)達(dá)到峰值���,隨壓強(qiáng)半徑
的增加�����,壓強(qiáng)值逐漸線性減小至0�。其中壓強(qiáng)峰值區(qū)域隨切向拉力線性增加����,達(dá)到壓強(qiáng)零值的半徑隨切向拉力線性降低���,如圖12(b)所示���。因此,需對(duì)線性壓強(qiáng)分布函數(shù)開展橫向�����、縱向壓強(qiáng)調(diào)整,以彌補(bǔ)切向外載荷造成的壓強(qiáng)變化����。
為建立不同切向拉力情況下的動(dòng)態(tài)變化分布函數(shù),需添加線性壓強(qiáng)函數(shù)縱向演化系數(shù)����。壓強(qiáng)峰值與切向拉力存在線性關(guān)系,因此可將壓強(qiáng)分布函數(shù)p(r)等比倍增����,其公式為
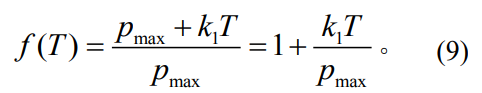
式中:pmax為T=0時(shí)的壓強(qiáng)峰值。
隨切向外力的增加�,壓強(qiáng)值達(dá)到零值時(shí)的半徑線性減小,通過有限元提取最大半徑的距離�,可得出斜率值。因此�,依據(jù)線性函數(shù)對(duì)壓強(qiáng)分布函數(shù)進(jìn)行橫向調(diào)整,其橫向半徑長度之比為式中:
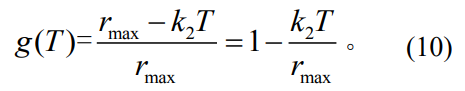
rmax為T=0時(shí)的最大接觸半徑����。
因此,隨切向載荷變化的線性壓強(qiáng)分布函數(shù)為
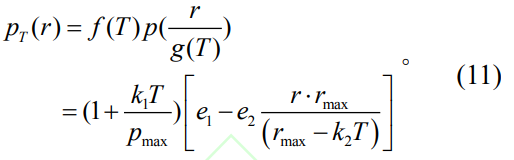
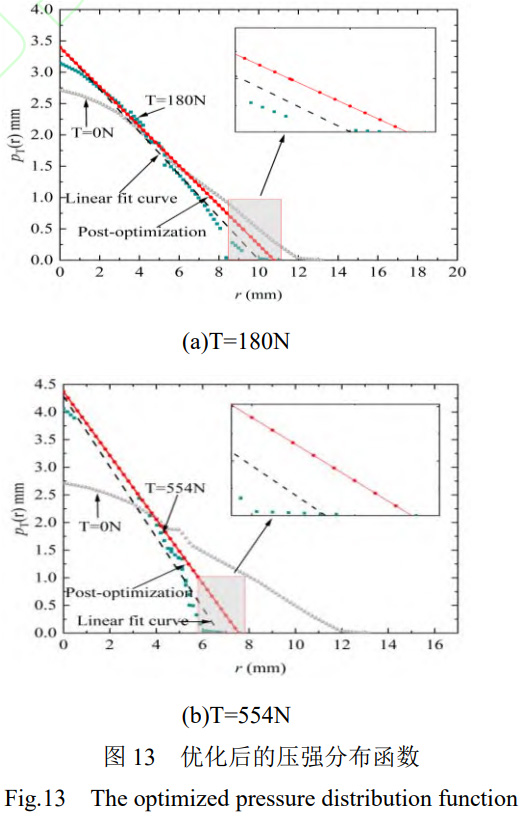
T=180N�����、554N切向拉力下的壓強(qiáng)分布曲線,如圖13所示�����。當(dāng)壓強(qiáng)為峰值時(shí)��,優(yōu)化后的動(dòng)態(tài)壓強(qiáng)分布函數(shù)與原動(dòng)態(tài)壓強(qiáng)的擬合函數(shù)具有較高的重疊度��。當(dāng)壓強(qiáng)為零時(shí)��,優(yōu)化后的函數(shù)半徑較大于原函數(shù)的擬合曲線�����,其半徑分別為:10.77675mm�、10.02866mm和7.5789mm、6.7168mm���,兩條曲線在壓強(qiáng)為零時(shí)存在一定偏差,但總體擬合效果較好���,證明了本文動(dòng)態(tài)線性壓強(qiáng)分布函數(shù)的準(zhǔn)確性�。
4、結(jié)束語
本文建立了簡(jiǎn)化的螺栓和等效平板有限元模型����,研究了螺栓連接結(jié)構(gòu)結(jié)合面的接觸邊界和壓強(qiáng)分布演化規(guī)律。結(jié)果表明:
(1)結(jié)合面接觸區(qū)域受切向力的影響發(fā)生動(dòng)態(tài)變化���。當(dāng)切向載荷較小時(shí)�,初始狀態(tài)接觸的螺孔周圍呈現(xiàn)圓形粘滯狀態(tài)��,伴隨切向力的施加����,粘滯區(qū)域逐漸減小,接觸形態(tài)由圓形逐漸演化為橢圓狀�����,未達(dá)到最大長半軸�����。當(dāng)切向載荷較大時(shí)���,接觸區(qū)域由粘滯狀態(tài)逐漸過渡至滑移狀態(tài)�����,滑移區(qū)域不斷從外部向內(nèi)部延伸�,x方向滑移長度縮短,y方向滑移長度增加����,接觸區(qū)域超過平板邊界,平板對(duì)接觸區(qū)域產(chǎn)生“截?cái)唷爆F(xiàn)象���。
(2)切向載荷作用下�,結(jié)合面各點(diǎn)的壓強(qiáng)發(fā)生變化����。采用線性壓強(qiáng)分布函數(shù),對(duì)曲線進(jìn)行橫����、縱調(diào)整,得到表征效果較好����、參數(shù)較少的線性動(dòng)態(tài)壓強(qiáng)分布函數(shù)�����。為螺栓連接結(jié)構(gòu)的性能評(píng)估提供理論支撐。
參考文獻(xiàn)(References)
[1] WANG Shengao, ZHU Min, CAO Hongjun, et al. Contact Pressure Distribution and Pressure Correction Methods of Bolted Joints under Mixed-Mode Loading[J]. Coatings, 2022, 12(10): 1516.
[2] 宋道遠(yuǎn), 徐興華, 邱少華, 等.基于改進(jìn) YOLOv5 的螺 栓 緊 固 件 檢 測(cè) [J]. 海 軍 工 程 大 學(xué)學(xué) 報(bào) , 2024,36(3):72-76.
SONG Daoyuan, XU Xinghua, QIU Shaohua, et al. Bolt Fasteners Detection Based on Improved YOLOv5 [J]. Journal of Naval University of Engineering, 2024,36(3):72-76. (in Chinese)
[3] LU Xiaohan, ZHU Min, LI Chao, et al. Prediction of Pre-Loading Relaxation of Bolt Structure of Complex Equipment under Tangential Cyclic Load [J]. Sensors, 2024, 24(11): 3306.
[4] ZHANG Weihong, LI Jiajia, GAO Tong. Topology Optimization of Elastic Contact Problems with Maximum Contact Pressure Constraint [J]. Structural and Multidisciplinary Optimization, 2022,65(4): 106.
[5] ZHAO Binbin, WU Fayong, SUN Kepeng, et al. Study on Tangential Stiffness Nonlinear Softening of Bolted Joint in Friction-Sliding Process [J]. Tribology International, 2021, 156:106856.
[6] WANG Shengao, ZHU Min, XIE Xin, et al. Finite Element Analysis of Elastoplastic Elements in the Iwan Model of Bolted Joints [J]. Materials, 2022, 15: 5817.
[7] LI Dongwu, BOTTO Daniele, XU Chao, et al. A Micro-Slip Friction Modeling Approach and Its Application in Underplatform Damper Kinematics [J]. International Journal of Mechanical Sciences, 2019, 161-162: 105029.
[8] LI Dongwu, XU Chao, BOTTO Daniele, et al. A Fretting Test Apparatus for Measuring Friction Hysteresis of Bolted Joints [J]. Tribology International, 2020, 151: 106431.
[9] 趙永武, 呂彥明, 蔣建忠. 新的粗糙表面彈塑性接觸 模型[J]. 機(jī)械工程學(xué)報(bào), 2007,43(3): 95-101.
ZHAO Yongwu, LYU Yanming, JIANG Jianzhong. New Elastic-plastic Contact Model of Rough Surface[J]. Journal of Mechanical Engineering, 2007,43(3): 95-101. (in Chinese)
[10] MOTOSH N. Determination of Joint Stiffness in Bolte Connections [J]. Journal of Engineering for Industry, 1976, 98(3): 858-861.
[11] JOHNSON K L. Contact Mechanics [M]. Cambridge: Cambridge University Press, 1985:84-106.
相關(guān)鏈接